A pesar de la innumerable evidencia que existe al respecto, aún hay quienes sostienen que la Tierra es plana.
Ésto ha llevado incluso al reconocido empresario espacial Elon Musk a referirse al tema en redes sociales, a través de una irónica pregunta.
“¿Por qué no existe ninguna Sociedad de Marte Plano?”, escribió el sudafricano en su cuenta de Twitter hace unos meses.
Y aunque la mayoría sabe que la Tierra efectivamente es redonda, un usuario de Imgur tuvo un momento de duda luego de fotografiar el lago Michigan.
Se trata de Greg, un músico de 47 años y residente de la ciudad norteamericana de Manitowoc, quien tras ver la fotografía, notó que el horizonte se veía demasiado plano.

“He mirado el horizonte de ese lago miles de veces y me preguntaba si se veía la curvatura. No lo sé, quizá un poco, o quizá me engaña la mente”, señaló al portal de virales Bored Panda.
Y es que sin importar cuánto zoom hacía, o si recurría al modo panorámico, el horizonte continuaba viéndose totalmente plano.

Fue así como el hombre decidió recurrir a la ciencia, y a Google Earth, para encontrar una respuesta a su duda.
En la siguiente imagen aparece marcado en verde el punto exacto desde el cual Greg tomó la fotografía, mientras que las costas de Two Rivers y la de Silver Creek Park están en amarillo.
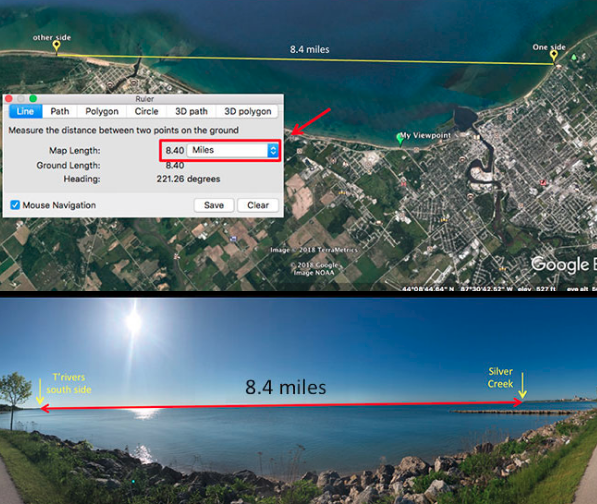
Gracias al programa de Google, Greg determinó que la distancia entre ambas playas es de 8,4 millas, o 13,5 km.
Lo que hizo entonces, fue determinar cuánto equivale este número en comparación a la circunferencia de la Tierra, además de calcular la curvatura de este trozo.
Según sus cálculos, si la circunferencia de nuestro planeta es de 25.000 millas (40.000 km), las 8,4 millas tendrían un arco de 0,12 grados.
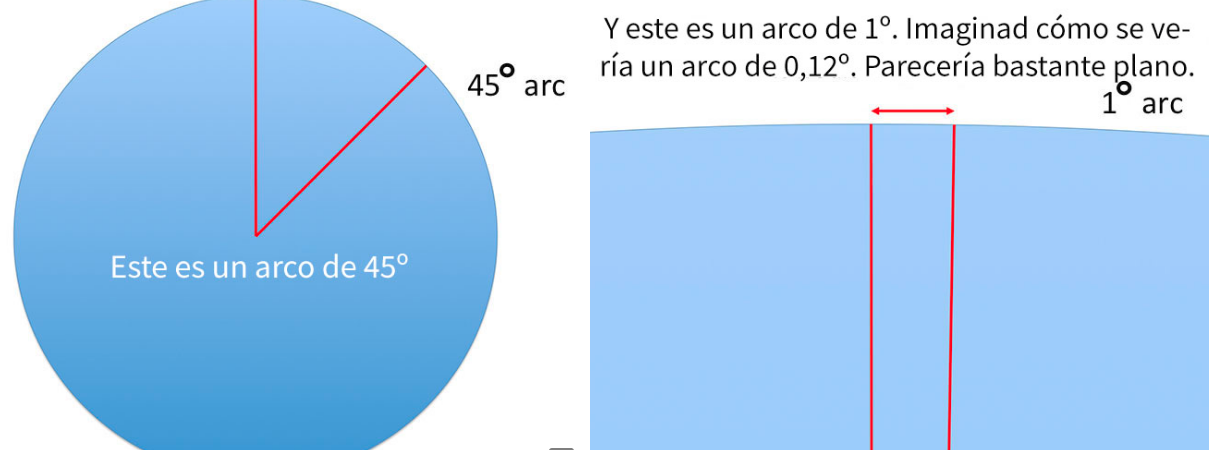
En su afán por apreciar la curvatura de un arco de sólo 0,12 grados, Greg determinó que sería sencillamente imperceptible.
Dicho de otro modo, por muy redonda que sea la Tierra, notar su curvatura parado en una playa es imposible.

De hecho, según un artículo del sitio Muy Interesante, recién a partir de los 10.000 metros de altura -similar a la altura en la que vuelan los aviones- veríamos el horizonte con una cierta curvatura.
“Para ver bien la curvatura terrestre habría que volar bastante más arriba, quizá por encima de los 15.000 metros. A 20.000 ya es claramente perceptible”, agrega el citado medio.
Si bien es cierto que en algunas imágenes tomadas desde menor altura se aprecia el horizonte curvado, esto se debe a la distorsión generada por los lentes de las cámaras.